[ HTML | PDF (web) | PDF (print) ]

4. The Disparity Map

As described in the introduction, the bulk of this thesis addresses the issue of cloth motion capture. In this chapter, some of the details of the first stage of the cloth motion capture system are discussed, covering the construction of a disparity map from input multibaseline stereo images.

The output of this stage of our system is three images of equal size: a rectified greyscale camera image of the cloth and backdrop; a mask to distinguish the cloth from the backdrop; and a disparity map, from which the depth at every pixel can be inferred. The greyscale image and disparity map can be generated with a standard stereo vision system, and the mask can be easily defined using background subtraction.

Rectified images and epipolar geometry are a well-understood subject in computer vision. Given a suitable system for camera calibration, it is easy to produce rectified images [84]. Stereo correspondence algorithms take two (or sometimes more) rectified greyscale images as input, and produce a disparity map d(x,y) for each pixel in one of the input images, typically stored as a greyscale image. Figure 4.1 demonstrates this process, although the disparity map shown here is somewhat idealised. The term disparity was originally used to describe the 2D vector between the positions of corresponding features seen by the left and right eyes. It is inversely proportional to depth, and it is possible to define a mapping from an (x,y,d) triple to a three-dimensional position.

Figure 4.1: Stereo correspondence algorithms take two (or more) rectified images as input and produce a disparity map.

There are a wide range of stereo correspondence algorithms. We refer the reader to the excellent survey by Scharstein and Szeliski [97,98,99] for a taxonomy of the available techniques. We used the Sum of Absolute Differences (SAD) correlation method to reconstruct disparity maps. This is a very simple approach with a number of major artefacts, and in the remainder of this chapter we discuss our solutions to the shortcomings of SAD correlation. However, it should be noted that a more sophisticated stereo correspondence algorithm (such as the graph cuts approach) might be a more suitable solution, and could be easily substituted.

The SAD correlation method yields three major types of artefacts. First, in some regions disparities are uncertain, and are left as "holes'' in the disparity map, as demonstrated in Figure 4.2(a). Uncertainty can occur for a variety of reasons, including insufficient texture, depth discontinuities or noisy images.

Figure 4.2: (a) original disparity map with holes; (b) hole-filled integer disparity map; (c) after sub-pixel estimation. Intensity levels have been exaggerated to emphasise quantisation.

(a)	(b)	(c)

Second, most disparity maps are only computed to integer precision, i.e. $d(x,y) \in \mathbb{Z}$. When these disparities are inverted to obtain depth, the resulting depthmap is visibly quantised, yielding a very jagged surface. Some algorithms attempt to calculate a fractional part for each disparity using sub-pixel estimation, but such techniques are still tentative and can produce incorrect results [100]. An example of the errors corrected by sub-pixel estimation is shown in Figure 4.2(b).

Third, window-based stereo correspondence algorithms often exhibit a "foreground fattening'' effect near depth discontinuities between two objects. When this happens, samples from the far object are mistakenly measured as having the same disparity as samples on the near object, as demonstrated in Figure 4.3.

Figure 4.3: Demonstration of the foreground fattening effect: (a) input image, with foreground cloth on left and black background. (b) disparity map produced by stereo correspondence algorithm.

(a)	(b)

The stereo system we used is prone to all three of these problems. We have developed a technique that smoothly fills holes and finds a fractional part to each disparity to create a smoother surface, but we have no way to solve the problem of foreground fattening. The fractional part is not measured from the input images, as in the traditional sub-pixel estimation algorithms used by the vision community, but is instead smoothly interpolated from the measured integer disparities.

We do not claim that our solution is a novel contribution to the field; we merely document our approach in the interest of thoroughness. Our solution is adapted to the particular needs of the stereo system we used, but it is likely possible to find an existing stereo system that exhibits none of these problems. In the future, we expect that standard stereo systems will solve these problems, and output from a stereo system can be used directly without the modifications described here.

We have the option of operating on either the two-dimensional disparity map, or the corresponding three-dimension surface. Given the structured nature of our input data, we choose to operate directly on the disparity map in a two-dimensional manner for the sake of efficiency.

4.1 The PDE Approach

Both hole-filling and sub-pixel estimation can be formulated as image interpolation problems. Image interpolation is an image-based technique that involves filling holes in an image with plausible data. The hole is not necessarily filled with smooth data, but may sometimes involve extending discontinuities at the hole edge into the hole. It has been well studied by researchers such as Bertalmio et al. [10], Caselles et al. [26] and Pérez et al. [86], and is also studied as part of the larger problem of image inpainting. The general approach involves fixing the boundary of the hole, and then solving a boundary-value partial differential equation (PDE) to interpolate the interior of the hole. This is equivalent to applying a diffusion process, such as isotropic diffusion or one of the many forms of anisotropic diffusion. For more details on isotropic and anisotropic diffusion, refer to Black et al. [12]. For a detailed description of the relation between diffusion and partial differential equations, see Sapiro's excellent book [96].

Caselles et al. also considered a different problem. They started with a quantised image, i.e. only a limited set of intensity values, such as multiples of 30. From this, they wished to produce a smooth image with integer intensity values using an image interpolation algorithm. This would also produce a satisfactory solution to our sub-pixel estimation problem; the disparity map can be viewed as a quantised image, and smooth interpolation of the data would be a satisfactory solution.

Caselles' approach can be explained using a one-dimensional example, as shown in Figure 4.4. Suppose that the image I(x) is quantised to image I_q(x) by rounding image intensities to the nearest integer multiple of δ. We aim to interpolate I_q(x) to form a smooth interpolated image I_i(x). Consider two adjacent points, x₀ and x₁ at a step edge, $I_q(x_1)=I_q(x_0) + \delta$. Clearly, the intensity of the unquantised image $I$ crossed the mid-intensity point $I_q(x_0) + \frac{\delta}{2}$ somewhere between x₀ and x₁. We can take advantage of this and force the high point of each step edge down to the mid-intensity point, i.e. fix $I_i(x_1)=I_q(x_0) + \frac{\delta}{2}$. Finally, these fixed points are interpolated. A special case is required for step edges larger than δ, in which case both the high and low side of the edge are fixed. Extension to a two-dimensional image is straightforward, with the fixed points forming closed Jordan curves in the plane. Caselles called these the boundaries of the level sets, but it should be noted that his level sets are not directly related to standard levelset methods in computer graphics [83].

Figure 4.4: (a) one-dimensional example of Caselles' approach, with black showing quantised disparity map and red showing disparity map after interpolation using diffusion; (b) boundaries of level sets in two-dimensional case.

(a)	(b)

We implemented Caselles' approach, using a simpler isotropic diffusion process for both hole-filling and interpolation of the quantised disparity map. An isotropic diffusion process finds a solution to

$$\nabla^2(I) = 0,$$ (4.1)

which is also known as Laplace's equation. Laplace's equation is a special case of Poisson's equation, and is a classic example of an elliptic PDE. In this formula, the $\nabla ^2$ operator is the Laplacian, where

$$\nabla^2(I) = \operatorname{div}(\nabla I).$$

Implementation of this approach was quite straightforward. The PDE was solved by using an explicit integration scheme, with

$$I(t + \Delta t) = I(t) + \Delta t \frac{\partial I}{\partial t}$$

where

$$\frac{\partial I}{\partial t} = \nabla^2\left( I(t) \right).$$

and $\Delta t = 1$. To improve performance, a hierarchical approach was used, solving first on a low-resolution image, then using those results as the starting point for diffusion on a higher-resolution image.

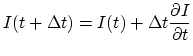
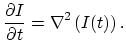
Initially, the results from this approach seemed reasonable. Performance was quick, requiring only about two minutes per frame. Holes were smoothly filled, showing C⁰ continuity and C¹ continuity with the fixed hole boundary. Quantisation artefacts were resolved, with C⁰ continuity. However, there were C¹ continuity problems at the fixed boundaries of the level sets used to interpolate the quantised disparity map. The diffusion process did yield C¹  continuity on either side of the levelset boundary line, but the derivatives on either side of the boundary were not identical. Consequently, the image gradient had clearly visible discontinuities along the boundaries of the level sets.

Ultimately, more control was needed at the boundaries during diffusion. Like Caselles, we fixed the value of the function at the boundary, known in the PDE literature as imposing Dirichlet conditions on the boundary value partial differential equation. Cauchy conditions are a standard alternative, where both the value and the gradient are specified at the boundary as described in [87]. Unfortunately, Cauchy conditions cannot be used, since the gradient at the boundary is unknown; we only want the gradient on either side of the levelset boundaries to be the same. It is possible that the biharmonic equation could provide this control over the system, but we leave this as future work.

4.2 The Optimisation Approach

PDE methods were satisfactory for hole-filling, but could not solve the sub-pixel estimation problem. Using a diffusion-based approach, the only way to interpolate the existing data to perform sub-pixel estimation was by introducing fixed boundaries of the level sets. However, the interpolation can be achieved in a different manner.

As before, a solution to Laplace's equation (Equation 4.1) is desired, starting from a variant,

$$\nabla^2(I + \Delta I) = 0,$$ (4.2)

with I held constant and solving for ΔI. A strict interpolation of the quantised data can be achieved by constraining ΔI to lie between $-\frac{\delta}{2}$ and $\frac{\delta}{2}$. Under this constraint, an exact zero solution to Laplace's equation may not be found, but the equation can be solved in a least-squares sense. In other words, find ΔI that minimises

$$\sum_{x,y} \left[\nabla^2\left(I_{x,y} + \Delta I_{x,y}\right)\right]^2$$ (4.3)

subject to $-\frac{\delta}{2} \leq \Delta I_{x,y} \leq \frac{\delta}{2}$. This is an optimisation problem, not a partial differential equation problem.

We use a finite-difference representation of the Laplacian,

$$\begin{multline} \nabla^2(I + \Delta I) = ( I + \Delta I )_{x,y-1} + ( I + \... ...x-1,y} + ( I + \Delta I )_{x+1,y} \\ - 4( I + \Delta I )_{x,y}. \end{multline}$$

With a little juggling and remapping of indices, this can be expressed as a linear system

$$\mathbf{Ax}=\mathbf{b}.$$

The image ΔI is flattened to form the vector x. Suppose that ΔI is w pixels wide by h pixels high. Then, the first w entries of x are filled with the top row of ΔI, followed by the second row, and so on. The constant coefficients of ΔI are placed in the A matrix, and the constant I values are placed in vector b.

Figure 4.5: General structure of A matrix used by optimisation approach for sub-pixel estimation. The neighbour count a_i is equal to the sum of the other elements of the row (typically 4).

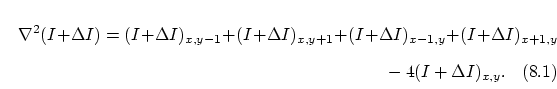
As shown in Figure 4.5 the matrix A is sparse with the standard 5-point Laplacian structure, sometimes known as "tridiagonal with fringes.'' The main diagonal represents the central count in the finite-differencing scheme, the upper and lower diagonals correspond to the right and left neighbours respectively, and the fringe diagonals correspond to the lower and upper neighbours. The value a_i on the main diagonal is initially adjusted to ensure that the sum of each row is zero.

The problem can now be expressed in a simple, classic form. Find x that minimises

$$\lvert\lvert\mathbf{Ax}-\mathbf{b}\rvert\rvert ,$$ (4.4)

subject to $-\frac{\delta}{2} \leq \mathbf{x}_i \leq \frac{\delta}{2}$

This is a constrained linear least-squares minimisation problem. We use Matlab to solve this equation, and Matlab uses a subspace trust-region method based on the interior-reflective Newton method, as described by Coleman et al. [29].

Some small modifications are made to this scheme for practical purposes. Not all entries in I are valid, and this must be accounted for. Invalid samples are excluded from both the A and b matrix. We adjust the central count a_i to include only the number of valid neighbour samples. Finally, for hole-filling, the boundary values surrounding the hole are included in b but excluded from A.

In practical terms, this algorithm performs quite slowly. A hierarchical version performs much better, and some minor edits to Matlab's source files can improve performance to about three minutes per frame. The appearance of the results is satisfactory, exhibiting both C⁰ and C¹  continuity.

As noted before, the optimisation approach is only needed for sub-pixel estimation. Both the PDE and optimisation approaches produce satisfactory results for hole-filling, and the PDE approach yields better performance.