[ HTML | PDF (web) | PDF (print) ]

5. Parameterisation

The parameterisation of the cloth surface follows several stages, similar in principle to stages in many computer vision systems. First, features are detected in the intensity image. Each feature is then matched with features in a flat reference image of the cloth. The global structure of the parameterisation is analysed, and invalid features are rejected. Finally, parameter values are interpolated for every pixel in the input image.

5.1 Feature Detection

For feature detection, we use Lowe's Scale-Invariant Feature Transform (SIFT) [76,77]. Features detected using SIFT are largely invariant to changes in scale, illumination, and local affine distortions. Each feature has an associated scale, orientation and position, measured to subpixel accuracy. Features are found at edges using the scale-space image gradient. Each feature has a high-dimensional "feature vector,'' which consists of a coarse multiscale sampling of the local image gradient. The Euclidean distance between two feature vectors provides an estimate of the features' similarity. Lowe used SIFT features for the object recognition task, and considered only rigid objects with a very small number of degrees of freedom. See Brown and Lowe's 2002 paper [21] for an example of object recognition. An upcoming paper by the same authors [22] uses SIFT for image registration in panorama stitching, a very different problem. We make heavy use of SIFT features, but we must adapt the matching to the parameterisation of cloth, a deformable surface with a very high number of degrees of freedom.

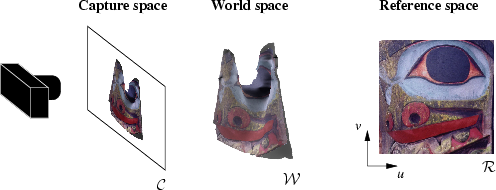
We detect features in two different images. A scan of the flattened cloth is used to obtain the reference image, a flat and undistorted view of the cloth. We use the 2D image coordinates of points in the reference image directly as (u,v) parameters for the features. This 2D parametric reference space is denoted $\mathcal{R}$. The second image is the input intensity image, called the captured image here. We refer to this 2D image space as the capture space, and denote it $\mathcal{C}$.

We also work in world space $\mathcal{W}$, the three-dimensional space imaged by the stereo system. Capture space is a perspective projection of world space, and the disparity map provides a discretised mapping from capture space to world space. We map disparity values at discrete locations back to world space and use linear interpolation to obtain a continuous mapping. Finally, we also work in the feature space $\mathcal{F}$. This is a 128-dimensional space containing the SIFT feature vectors for both the reference and the captured features.

Figure 5.1: Capture space $\mathcal{C}$ is an image of 3D world space $\mathcal{W}$. Reference space $\mathcal{R}$ is a flattened view of the cloth.

After applying SIFT to the reference and captured images, we obtain two sets of features,

$$\mathbf{F}_r =\{ r \,\vert\,\mathbf{p}(r) \in \mathcal{R}, \mathbf{f}(r) \in \mathcal{F} \}$$

$$\mathbf{F}_c =\{ c \,\vert\,\mathbf{p}(c) \in \mathcal{C}, \mathbf{f}(c) \in \mathcal{F} \}$$

where p(x) is the position of feature x within the image, and f(x) is the feature vector associated with x. Each feature also has an associated scale $\mathbf{s}(x) \in \mathbb{R}$. An example of these feature sets is shown in Figure 5.2.

Figure 5.2: (a) reference feature set $\mathbf{F}_r$; (b) captured feature set $\mathbf{F}_c$.

(a)	(b)

If we can establish a one-to-one mapping between reference features and captured features, then we know both the world space position and the reference space position of every captured feature, allowing parameterisation. In the matching stage of the algorithm described in Section 5.2, we construct this one-to-one mapping, which we label $\Phi :\mathcal{C}\to \mathcal{R}$. It should be noted that a one-to-one mapping is only feasible if the pattern in the reference image has no repetitions.

Cloth strongly resists stretching, but permits substantial bending; folds and wrinkles are a distinctive characteristic of cloth. This behaviour means that sections of the cloth are often seen at oblique angles, leading to large affine distortions of features in certain regions of the cloth. Unfortunately, SIFT features are not invariant to large affine distortions.

To compensate for this, we use an expanded set of reference features. We generate a new reference image by using a 2×2 transformation matrix T to scale the reference image by half horizontally. We repeat three more times, scaling vertically and along axes at $\pm$45°, as shown in Figure 5.3. This simulates different oblique views of the reference image. For each of these scaled oblique views, we collect a set of SIFT features. Finally, these new SIFT features are merged into the reference feature set. When performing this merge, we must adjust feature positions, scales and orientations by using $\mathbf{T}^{-1}$. This approach is compatible with the recommendations made by Lowe [77] for correcting SIFT's sensitivity to affine change.

Figure 5.3: Top row: a reference image and a horizontally scaled oblique view. Bottom row: other oblique views.

5.2 Matching

The Euclidean distance in $\mathcal{F}$ given by $\lvert\lvert\mathbf{f}(r)-\mathbf{f}(c)\rvert\rvert$ is the simplest metric for finding a match between a reference feature $r \in \mathbf{F}_r$ and a given captured feature $c \in \mathbf{F}_c$. Unfortunately, in our tests with cloth this metric is not sufficient for good matching, and tends to produce a sizable number of incorrect matches.

We would like to enforce an additional constraint while performing feature matching. The spatial relationship between features can help to eliminate bad matches: any pair of features that are close in reference space must have matches which are close in capture space. The converse is not always true, since two nearby captured features may lie on opposite sides of a fold. If we could enforce this capture/reference distance constraint during the matching process, we could obtain better results.

We can extend this notion by thinking about distances between features in world space. Suppose that we have complete knowledge of the cloth surface in world space (including occluded areas), and can calculate the geodesic distance in $\mathcal{W}$ between two captured features $c_s,c_n \in \mathbf{F}_c$:

$$\Delta d_c = g\left(c_s,c_n\right).$$ (5.1)

Now, consider two reference features $r_s,r_n \in \mathbf{F}_r$, which are hypothetical matches for c_s and c_n. We know the distance in $\mathcal{R}$ between r_s and r_n, but we do not know the distance between them in $\mathcal{W}$. By performing a simple calibration step, we can establish a scalar multiple relating distances in these two spaces. We will multiply by α_r to map a distance from $\mathcal{R}$ to $\mathcal{W}$, and multiply by α_r^-1 for the opposite mapping.

Using α_r, the world space distance between the reference features can be calculated.

$$\Delta d_r = \alpha_r \cdot \lvert\lvert\mathbf{p}(r_s)-\mathbf{p}(r_n)\rvert\rvert$$ (5.2)

We will use these two distances to define the compression constraint and the stretch constraint:

$$\Delta d_r(1 - k_s) < \Delta d_c < \Delta d_r(1 + k_s)$$ (5.3)

where k_s is a constant defining the maximum allowable stretch.

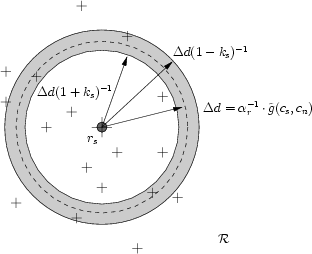
We refer to the lower bound on $\Delta d_c$ as the compression constraint, and the upper bound is called the stretch constraint. If $\Delta d_c > \Delta d_r(1+k_s)$, then this choice of match implies that the captured cloth is very stretched; similarly, if the compression constraint is violated, then this choice of match implies that the captured cloth is very compressed. Provided that a reasonable choice is made for k_s, we can safely reject matches that violate the stretch constraint or the compression constraint. Figure 5.4 illustrates these constraints.

Figure 5.4: If we fix two captured features c_s and c_n and one reference feature r_s, the stretch and compression constraints require the remaining reference feature to lie in a ring centred on r_s. The ring's inner and outer radii are derived from Equations 5.2 and 5.3.

In our real-world setting, finding the geodesic distance between captured features is more difficult. In situations where the entire cloth surface between c_s and c_n is visible, we define a straight line between c_s and c_n in $\mathcal{C}$, project this line onto the surface in $\mathcal{W}$, and integrate along the line. This will not find the geodesic distance, but will closely approximate it.

$$\Delta d_c = \tilde{g}(c_s,c_n)$$ (5.4)

While this tends to overestimate $g(c_s,c_n)$, it is still preferable to computing the actual geodesic distance, which is prohibitively expensive.

In some situations, sections of the cloth surface on the geodesic line between c_s and c_n will be occluded. We can detect such situations using the same line integration method as before, scanning for discontinuities in depth along the line. When occlusion occurs, there is no way of estimating the actual geodesic distance $g(c_s,c_n)$. However, we can still use $\tilde{g}(c_s,c_n)$, which in this case is likely to be an underestimate of $g(c_s,c_n)$. The stretch constraint can be applied to these features, but we cannot use the compression constraint, since the amount of fabric hidden in the fold is unknown at this point.

In contrast to the distance metric in feature space, the stretch and compression constraints are applied to pairs of matched features. To accommodate this, we adopt a seed-and-grow approach. First, a small number of seeds are selected, and these seeds are then matched using only the feature space distance metric. For each seed, we "grow'' outwards in capture space, finding nearby features and matching them. As we find features, we can use a nearby pre-matched feature to enforce the stretch constraint.

5.2.1 Seeding

The seeding process is straightforward. We select a small subset of captured features $\mathbf{F}_c' \subset \mathbf{F}_c$, and find matches for them in a brute force manner. For each $c \in \mathbf{F}_c'$, we compare against the entire reference feature set F_r, and we use the feature-space distance between c and $r \in \mathbf{F}_r$ to define the quality of a match. To improve the speed of the brute force matching, we use Beis & Lowe's best bin first algorithm [9]; this is an approximate search in a k-d tree. (It is approximate in that it always returns a close match, but not always the best match possible.) We then sort F_c' by the feature-space distance, and apply the growth process on each seed in order, from best-matched to worst. The growth process classifies captured features into three sets: matched, rejected and unknown. If a seed fails to grow, the seed itself is classified as rejected. After all seeds have been grown or rejected, we construct a new F_c' from the remaining unknown captured features.

To help the process, we prefer captured features with a large SIFT scale s(c) when selecting $\mathbf{F}_c'$. In the first iteration, $\mathbf{F}_c'$ consists of the largest features, followed by a smaller group, and so on until a minimum scale is reached. Large features are only found in relatively flat, undistorted, and unoccluded regions of the cloth. In these regions, the growth process will be able to proceed rapidly without encountering folds or occlusions, rapidly reducing the number of unknown features. This rapid growth reduces the number of features which must be considered as seed candidates. The use of the seeding process should be reduced as much as possible, since it cannot make use of the stretch and compression constraints, and hence must resort to relatively inefficient and unreliable brute force matching.

5.2.2 Growing

The growth process is controlled with a priority queue. Each entry in the priority queue is a matched source feature $c_s \in \mathbf{F}_c$ on the edge of the growth region. The queue is sorted by capture space distance from the seed, ensuring an outward growth from the seed. The queue is initialised with the seed point alone. The source features are extracted from the queue one at a time.

Let us consider one such source feature, consisting of c_s and $r_s = \Phi (c_s)$. To grow outwards, we iterate over all features c_n in the neighbourhood N(c_s) of c_s in capture space. N(c_s) is a circle of radius r_c centred on c_s. For a given c_n, the match candidates are the reference space features which pass the stretch and compression constraints. These candidate features lie in a ring around r_s, as shown in Figure 5.4.

To select the best match among the match candidates, we use the feature space distance $\lvert\lvert\mathbf{f}(c_n)-\mathbf{f}(r_n)\rvert\rvert$ for each candidate r_n. The closest match is accepted, provided that the distance in $\mathcal{F}$ is below a threshold.

The growth process requires knowledge of neighbouring features in capture space, and neighbours within a ring in reference space. We efficiently retrieve these neighbours by performing binning in a preprocessing stage.

5.3 Verification

The growth algorithm enforces constraints during the matching process, but it only works with two features at a time. A feature matched by the seed-and-grow process may be acceptable when compared with one of its neighbours, but it may be clearly incorrect when all neighbours are examined. During the growth process, however, it is difficult to perform any global verification, since information about the cloth is sparse and incomplete. After the seed-and-grow algorithm has completed, we can verify the accuracy of matches. At this stage, we will only reject bad matches, and will not attempt to make any changes to $\Phi (c)$.

We attempt to correct two types of errors in the matching process. In the following, we will refer to the features matched during growth from a single seed as a seed group. A feature error occurs within a seed group, when a few isolated features in the group are badly matched but the bulk of the group is valid. A seed error occurs when a bad seed is accepted, in which case the entire seed group is invalid. We propose a three-stage solution to deal with these errors.

The stages are very similar, so we describe the general operation first. We operate on the Delaunay triangulation of the captured features, and we use a voting scheme to determine the validity of features or seed groups. One vote is assigned to each outwards edge. For a feature, every incident edge is used; for a seed group, every edge connecting a seed group feature to a different seed group is used. The vote is decided by evaluating the stretch and compression constraints on the edge. Finally, we calculate a mean vote for each feature or seed group, and reject the features or seed groups with the poorest mean vote. We repeat the process until all features or seed groups pass a threshold mean vote.

In the first stage of verification, we operate on each seed group in turn, and consider only feature errors within that seed group. Subsequently, we consider only seed errors between the seed groups. Finally, we do a repeat search for feature errors, this time operating on the entire set of remaining features. Typically, this final stage helps to eliminate bad features at the edge of the seed groups.

The entire verification process could be formulated as a simulated annealing algorithm. This would have the benefit of a better theoretical grounding; a continuous measure of error instead of a pass/fail threshold; and it would be easier to extend to include different types of errors. A simulated annealing scheme might also be suitable for correcting interframe errors, improving temporal coherence. This is left as future work.

5.4 Geometry Parameterisation

Figure 5.5: After verification, we have dense, regular disparity samples and sparse irregular (u,v) samples. We interpolate the (u,v) samples to achieve a uniform regular sampling of both geometry and parameterisation.

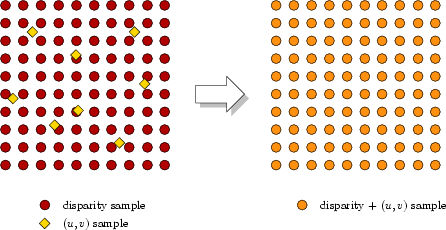After verification, we are left with a set of reliable features, and a dense, regularly sampled disparity map, as shown in Figure 5.5. We would like to construct a unified representation that contains both 3D and parametric data, sampled in the same pattern. We choose to interpolate the parametric information given by the features to construct a dense, regularly sampled parametric map corresponding directly to the disparity map.

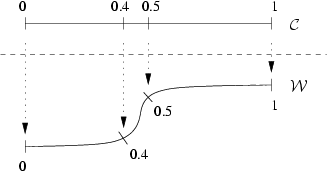
An interpolation in capture space is not sufficient, as demonstrated in Figures 5.6 and 5.7. As can be seen, linear interpolation in capture space leads to unacceptable distortions on the surface in world space. Instead, what is needed is linear interpolation along the surface (the arc in Figure 5.6). This must be extended from the one-dimensional example in the figure to a surface.

Figure 5.6: Example where linear interpolation of parameter values in $\mathcal{C}$ results in distortion of parameters when projected into $\mathcal{W}$.

Figure 5.7: Left: capture space interpolation. Right: our interpolation method.

This problem is similar in principle to the non-distorted texture mapping problem described by Lévy and Mallet [69] and others. Their technique enforced two primary constraints, perpendicularity and constant spacing of isoparametric curves on the surface. These goals are unfortunately not the same as our own: we desire constant spacing of isoparametric curves, but we would like to allow non-perpendicularity. In the language of the cloth literature, little or no stretch is permitted, while shearing may take place. Our problem is therefore subtly distinct from many of the standard problems in non-distorted texture mapping or mesh parameterisation.

First and foremost, we aim to perform a pure interpolation, retaining the parameterisation at all feature points. We choose to operate on individual triangles within the capture space Delaunay triangulation of the feature points. Within each such triangle the goal, like Lévy & Mallet, is to have constant spacing of isoparametric curves. We make no guarantees of C¹ or C² continuity across triangles.

Our interpolation scheme is recursive, and operates on a triangle mesh in capture space, typically a Delaunay triangulation of the input features. Parameters are known at every vertex of the mesh. Each triangle represents a curved surface patch, with the shape of the patch defined by the underlying disparity map.

We recursively subdivide each triangle into four smaller triangles using the standard 4-to-1 split, but with one slight difference. Instead of inserting new vertices at the capture space midpoint of each edge, we insert at the geodesic midpoint. In other words, if the endpoints of an edge are given by c₁ and c₂, the new vertex $v \in \mathcal{C}$ satisfies $\tilde{g}(c_1,v) = \tilde{g}(v,c_2)$ (where $\tilde{g}$ is the approximate geodesic distance from Equation 5.4), but it does not in general satisfy $\lvert\lvert\mathbf{p}(c_1)-v\rvert\rvert = \lvert\lvert v-\mathbf{p}(c_2)\rvert\rvert$. Since this point lies midway between the endpoints, its parametric position is the average of the endpoints' parameters. We form four new triangles using the three original vertices and the three new midpoint vertices, and proceed recursively on the smaller triangles.

The recursion stops when a triangle encloses exactly one disparity sample. At this point, the triangle can be treated as flat. To find the parameters at the disparity sample location, we associate barycentric co-ordinates with the sample location and linearly interpolate the parameters of the triangle's vertices.

This interpolation scheme still has several problems. It is possible that the correct interpolation between two features in $\mathcal{C}$ follows a slightly curved path in $\mathcal{R}$, instead of the straight line path used in this interpolation algorithm. The distortion caused by this approximation should be relatively subtle. More importantly, folds should receive special treatment during interpolation. In theory, it may be possible to make a reasonable guess about the world-space position of occluded regions hidden by the fold, but we leave this as future work.

The final issue in interpolation is finding an appropriate way to resist shearing. In our approach, shearing is not dealt with directly (as Lévy and Mallet did), but we are not certain that this is the best decision. Cloth permits shearing, but it does also resist it. Our scheme does not explicitly incorporate this behaviour. Any algorithm which does mix stretch and shear resistance will have to choose a means of balancing resistance to these two types of forces. It is hard to envision a suitable way of balancing stretching and shearing without some knowledge of the cloth material; we leave this as future work.