Feature Detection

The acquisition process produced three images: a colour image, a depth image, and a binary mask specifying which parts of the images contain valid data. These images contain information about both the cloth and the backdrop.

Colour and depth data contains some useful information about the properties of the underlying cloth. However, to understand the material properties and dynamic behaviour of cloth, more information is needed about the cloth surface. Topological information is needed in order to recover the shape of the cloth and to help with the identification of folds and wrinkles in the surface. Measurements of the surface deformation--stretch, shear and bend--can help with understanding the physical properties of the cloth material.

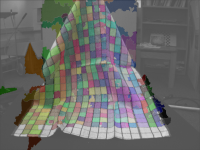
Recovering this information from the acquired data is a nontrivial task. To fully recover topology requires knowledge of sections of the cloth which may be occluded in the depth buffer by folds in the cloth. Measuring the exact stretch, shear or bend of the surface at any point is also a difficult task. To simplify the extraction of topology and deformation, a few simplifying assumptions were made. The cloth was assumed to be rectangular, with a grid pattern printed on it. By identifying the grid intersection points, a rough estimate of the cloth topology was established. Furthermore, by examining the distortion of the rectangles defined by the grid, the local surface deformation could also be estimated.

A similar approach has been used in cloth simulation. Baraff and Witkin [1] discretised a cloth surface into a triangular mesh, then measured the stretch and shear energy in each triangle, and the bend energy between pairs of triangles. These energies were used to determine forces to apply to the mesh vertices. In their paper, they consider the position of each mesh vertices in a flat, undeformed mesh in the (u,v) plane. Each vertex thus had two sets of co-ordinates: (u,v) co-ordinates defining its undeformed position, and (x,y,z) co-ordinates defining its actual position in three-dimensional space. Baraff and Witkin defined energy functions to measure stretching, shearing and bending in the cloth using this information.

I have adopted Baraff and Witkin's convention for co-ordinates. In this section, I summarise a technique for detecting grid vertices, and for then recovering (u,v) information.

Approach

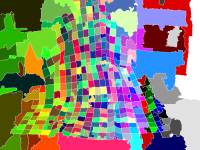
The grid pattern printed on the cloth had two overlaid grids, one in blue and one in yellow, printed on top of a white cloth. The yellow grid had poor contrast against the white background, so only the blue grid was used for extraction. This was accomplished by using only the red channel of the acquired colour image.

The grid vertex detection scheme depends upon two inputs: the red channel of the colour image, and a mask defining the valid regions in the image. The grid vertices were difficult to detect with conventional schemes, such as the SUSAN corner detector [13]. Instead, greyscale mathematical morphology techniques were used [10],[12]. MATLAB was used for all of these image-processing operations.

The overall strategy was to detect the squares bounded by the grid. For each square, the set of neighbouring squares was established. Using these neighbours, the set of squares bounding each corner could be determined. Finally, the corners were detected by finding the point that was minimally distant from each square.

Square Detection

In a first pass, the squares bounded by the grid are detected using the watershed transform introduced by Beucher [2]. The intuitive explanation for this transform involves picturing the image as a heightfield, where intensity represents height. In this terrain, there are a number of catchment basins (local minima). If one imagines slowly rising water emerging from the bottom of each basin, eventually the water will reach a stage where two catchment basins merge. The points where the basins merge form "watershed lines". The watershed transform uses this analogy to label each independent catchment basin in the input image, and to identify all watershed lines.

For the detection of grid points, the squares bounded by the grid were treated as catchment basins, and the grid lines are the watershed. The image was inverted, so that the white squares became valleys and the dark grid lines became peaks. Contrast enhancement was used to amplify the difference between peaks and valleys. Using a thresholding operation (the extended-minima transform), most of the valleys were forced to zero. Finally, the watershed transformation was applied. The combination of the extended-minima operation and the watershed transformation is equivalent to a watershed-from-markers operation.

The watershed transform labels pixels in each catchment basin with a unique value, as shown in Figure 3. There are a number of incorrect small basins, typically caused by aliasing artefacts near the two thick vertical stripes. By calculating the area of each catchment basin and rejecting basins below a minimum size, these can be eliminated. A dilated version of the mask was used to eliminate basins outside the mask.

**Figure 3:** Left: colour-coded output of watershed algorithm. Right: colour-coded watershed image, with mask applied and small basins rejected, superimposed on red channel of colour image.

Some errors are evident: adjacent squares were sometimes merged, and individual squares were sometimes split. By adjusting the threshold used in the extended-minima transform, it was possible to prefer more merging errors and less splitting errors, or the opposite. In the end, splitting errors were found to be preferable to merging errors.

Neighbourhood Detection

To find the neighbours of a given square, the following procedure was used. The watershed image provided a mask for the square, indicating all pixels belonging to the square. A residue mask was constructed by dilating the square mask with a two-pixel radius disc, and then subtracting the square mask. This residue mask was in turn used with the watershed image to find the neighbouring squares, as demonstrated in Figure 4. Neighbours with many pixels in the dilated mask shared an edge, and were part of the 4-neighbourhood of this square. Neighbours with only a few pixels in the dilated mask probably share a corner with this square, but not an edge, and were hence part of the 8-neighbourhood of the square. The process was repeated with a larger-radius disk for the mask dilation, to find all of the 8-neighbours of the square. For better performance, all of these operations were performed on a cropped image.

**Figure 4:** Top row: watershed + colour image around square, square mask. Bottom row: residue mask, residue mask + watershed + colour image.

Corner Detection

The corner detector takes a list of squares

as input, and finds the point which is "closest" to all four squares. To be precise, it finds the point

that minimises

**Figure 5:** First row: distance transforms of four corners. Black is zero distance, white is ten pixels' distance. Second row: maximum of distance transforms. The measured position of the corner is the darkest point in this image.

To obtain the list of squares for input to the corner detection routine, a slightly ad hoc strategy was necessary. First, a set of four squares was tried: a reference square, two of its 4-neighbours, and one diagonal 8-neighbour. By using a radial sort of the neighbours, these squares were guaranteed to share a corner. If this failed due to a missing neighbour, it was retried with two 4-neighbours, or one 4-neighbour and an 8-neighbour. If only a single 4-neighbour was available, no corner was measured.

The final set of corners is shown in Figure 6. As can be seen, there are a number of incorrect corners. These are mostly due to the choice of threshold in the watershed stage. By preferring splitting to merging, less false negatives are obtained, but more false positives are generated. Even still, there are a handful of corners that were not detected. There are a number of techniques that could remedy this: repeated attempts with different thresholds in the watershed stage could help, as could detection of corners in the case where only a 4-neighbour was available.

**Figure 6:** Red channel of colour image with detected corners superimposed.
$\begin{figure}\includegraphics[width=7cm]{cornersraw} \end{figure}$

Specification of (u,v)

In order to associate a (u,v) co-ordinate with each of these points, user interaction was required. The user was shown a point and asked to enter its position on the grid (an integer number of squares from the bottom left corner), which was then mapped to a (u,v) value in the unit square. The user was also able to reject incorrect corners.