Next: 6 Results Up: Implementing Baraff & Witkin's Previous: 4 Verification
Equations (54) and (57) are very different
from the equations obtained by Macri. Macri differentiated equations
(28) and (29)
and then rearranged to obtain two different formulas for
![]() :
:
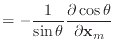 |
||
|
and
| ||
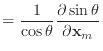 |
||
Likewise, Macri obtained two different formulas for
![]() .
Macri suggested choosing the first set of equations if
.
Macri suggested choosing the first set of equations if
![]() . The rationale
for this choice is presumably to avoid numerical problems and division by zero
when
. The rationale
for this choice is presumably to avoid numerical problems and division by zero
when
![]() . In order for the transition from one regime to the other
to be smooth, they should be equal at some changeover point. However, it is
not evident that there exists any changeover point where the two formulas are
equal. Additionally, neither of these equations matches
the numeric derivative of
. In order for the transition from one regime to the other
to be smooth, they should be equal at some changeover point. However, it is
not evident that there exists any changeover point where the two formulas are
equal. Additionally, neither of these equations matches
the numeric derivative of ![]() . My equations, however, give a result
identical to the numeric derivative.
. My equations, however, give a result
identical to the numeric derivative.
Macri's approach fails because he doesn't consider the transition between his two bend formulas. My approach succeeds in these cases because it relies on a single formula for all bend angles, instead of switching between formulas at critical bend points.
I derived equation (54) by the following logic. Define
![]() , and
, and
![]() . Then,
. Then,
![]() . Differentiating
. Differentiating ![]() , we obtain
, we obtain
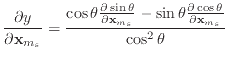
and thus,
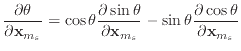
The derivation of (57) follows directly from differentation of this equation. In some ways, this definition feels a little circular due to the introduction of the artifical
I believe that there is a very small error in equation (14) of Baraff &
Witkin's paper: the ![]() term should be scaled by
term should be scaled by ![]() .
.
There is an error in their definition of
![]() , just above equation
(11). They define it as
, just above equation
(11). They define it as
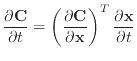
However, the condition function
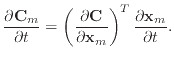
However, this yielded incorrect results, especially when calculating the damping forces for the bend condition, resulting in frequent instability. Later, I realised that correct application of the chain rule should yield a single
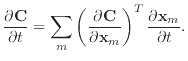 |
(58) |
The final error in their paper is related to scale-invariance. Ideally, the
parameters used for the simulation should be independent of the tesselation of
the surface. For example, if you run the simulation with a
![]() mesh and a
mesh and a
![]() mesh and the same parameters, it should look
basically the same. However, using Baraff & Witkin's choice of
mesh and the same parameters, it should look
basically the same. However, using Baraff & Witkin's choice of ![]() ,
this does not occur. I looked at the math for the specific case where the
number of particles is doubled in
,
this does not occur. I looked at the math for the specific case where the
number of particles is doubled in ![]() and
and ![]() (e.g., from
(e.g., from
![]() to
to
![]() ). In this case, the gravity force on each original particle
decreases by a factor of four (since the mass of the surrounding triangles
decreases by four). However, the (strong) stretch and shear forces decrease by
a factor of eight. These forces are responsible for most of the resistance
against gravity, and consequently the cloth sags substantially as the particle
density is increased.
). In this case, the gravity force on each original particle
decreases by a factor of four (since the mass of the surrounding triangles
decreases by four). However, the (strong) stretch and shear forces decrease by
a factor of eight. These forces are responsible for most of the resistance
against gravity, and consequently the cloth sags substantially as the particle
density is increased.
However, by using
![]() , the stretch and shear forces also
decrease by a factor of four, as expected. The formula is not as intuitively
obvious as
, the stretch and shear forces also
decrease by a factor of four, as expected. The formula is not as intuitively
obvious as ![]() , and I have not done tests with irregularly triangulated
meshes, but it does work much better for regularly triangulated meshes.
, and I have not done tests with irregularly triangulated
meshes, but it does work much better for regularly triangulated meshes.
During my original development, I chased down one wrong alley while looking for the error in my (and Macri's) derivations. I was highly suspicious of one of Baraff & Witkin's approximations, where they assume that vectors' magnitudes are constant. This occurs in both the shear condition derivation and the bend condition derivation. I went through and rederived all of the formulas without this assumption, and obtained the formulas given in the appendix. After all of this work, there was still a problem, which proved to be the error in Macri's versions of equations (54) and (57).
After finding this error in Macri's work, I returned to the unit magnitude issue. I compared the results of my simulation using the formulas given in the body of the paper (using Baraff & Witkin's approximation) to the results using the formulas given in the appendix (without the approximation). In my test case, I found that the approximation gave more pleasing results! In total, stretch energy was halved, and shear and bend energy dropped by a small amount. The formulas for both stretch and bend energy are unchanged between the two cases, so this is a valid comparison of the energy in the cloth. The formula for shear energy is slightly changed by removing the unit magnitude approximation, however, so comparisons of energy aren't very meaningful.
To be honest, I was surprised that such a drastic change to the formulas had a relatively small effect on the final result. I suspect that there may be a lot of room for optimisation of Baraff & Witkin's system, achieving comparable results at less computational cost.
In the interests of presenting a direct implementation of Baraff & Witkin's paper, and on the basis of the better results, I have therefore presented the formulas with the constant magnitude approximation.
For parameters, I adopted values that gave good results. I looked at
Alias ![]() Wavefront's Maya cloth software, but I suspect that they scale
their parameters internally by an unknown amount. For damping forces, I
multiplied the associated regular force's constant by the damping constant
(e.g.
Wavefront's Maya cloth software, but I suspect that they scale
their parameters internally by an unknown amount. For damping forces, I
multiplied the associated regular force's constant by the damping constant
(e.g.
![]() was used to damp stretch forces).
was used to damp stretch forces).
|