Next: 5 Discussion Up: Implementing Baraff & Witkin's Previous: 3 Condition Functions
Macri didn't describe any way of verifying the correctness of his derivations or implementation. Once I had initially implemented the simulator, I found bugs but had no way of determining where an error was occurring. To address this, I used numeric derivatives.
For example, suppose that we need to verify the calculation of
![]() . Our program calculates the derivative using an analytic
formula, which we'll call
. Our program calculates the derivative using an analytic
formula, which we'll call ![]() . The derivative can also be calculated
numerically:
. The derivative can also be calculated
numerically:
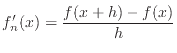
If
Verification is a little bit trickier for the bend condition. Here, we can't
just use a normal derivative, since we have to differentiate under the
assumption that the vectors have constant magnitude. Suppose that we want
to verify the derivative
![]() . Let
. Let
![]() represent
the normal with point
represent
the normal with point ![]() at position
at position
![]() , and
, and
![]() represent the normal once point
represent the normal once point ![]() 's
's ![]() th component is shifted by
th component is shifted by ![]() .
The unit normals are then given by
.
The unit normals are then given by
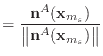 |
||
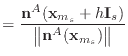 |
 |
To be honest, I don't know why numeric derivatives can't be used for everything. I suspect that they may be less robust than analytic derivatives, and there may be a performance tradeoff involved, but I haven't confirmed these suspicions.