Up: Implementing Baraff & Witkin's Previous: Bibliography
The equations given in this appendix are replacements for certain equations given in the body of the paper. By using these, several of Baraff & Witkin's approximations are avoided. However, my tests show that the results are less pleasing.
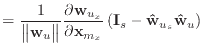 |
(A.1) | |
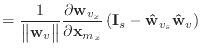 |
(A.2) |
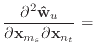 |
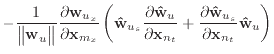 |
|
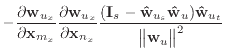 |
(A.3) | |
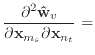 |
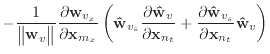 |
|
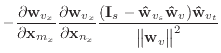 |
(A.4) |
If we remove the assumption that the
![]() and
and
![]() vectors are
unstretched, then equation (19) should be replaced with
vectors are
unstretched, then equation (19) should be replaced with
| (A.5) |
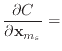 |
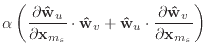 |
(A.6) |
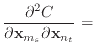 |
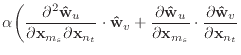 |
|
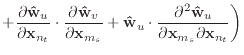 |
(A.7) |
If we remove the assumption that the normal and edge vectors have constant length, we must replace equations (40) and (43) with those shown below.
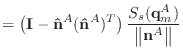 |
(A.8) | |
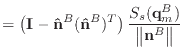 |
(A.9) | |
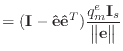 |
(A.10) |
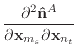 |
||
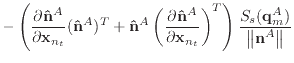 |
||
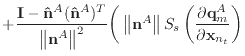 |
||
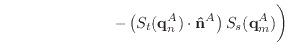 |
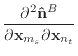 |
||
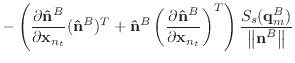 |
||
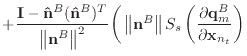 |
||
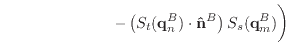 |
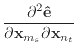 |
||
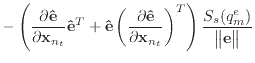 |
||
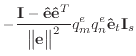 |
(A.11) |