[PDF | discussion]
Advances in Population Synthesis
10.1007/s11116-011-9367-4
David R. Pritchard
drpritch@gmail.com
Eric J. Miller
Date: Author's preprint version. The final publication is available
at
http://www.springerlink.com/openurl.asp?genre=article&id=doi:10.1007/s11116-011-9367-4
Key words and phrases: iterative proportional fitting - population synthesis - microsimulation - agent-based - census microdata - transportation models - trip forecasting
Agent-based microsimulation models forecast the future state of an aggregate system by simulating the behavior of a number of individual agents over time. These models are attracting interest from many fields, including activity-based travel demand modeling. The model output is usually the spatial arrangement of travel patterns (including the mode of travel used), and the agents are usually persons, families or households. The execution of such a model can be divided into two steps: the creation of an initial set of agents, their attributes and the system's state at some initial time; and a series of subsequent steps forward, where the state of each agent and the system as a whole is advanced by a timestep (for example, one year per step).
The relationships between agents are also important. For example, members of a household do not act entirely independently; they share resources and may choose to travel together in a single vehicle, to adjust their travel patterns to suit each others' schedules, or to make decisions about home ownership based on all household members' needs. In an integrated land use/transportation model, major decisions such as household relocation are intimately linked to the behavior of persons in the household. Consequently, it is also important to have accurate relationships between agents and a realistic grouping of persons into households. The spatial distribution of attributes also needs to be accurate at both the household level and the person level.
Unfortunately, the census data often used to support microsimulation models does not make this possible. For privacy reasons, many national censuses remove spatial detail when providing detailed information about particular households or persons. In some countries, linkages between households and persons are also stripped. Consequently, “population synthesis” methods are necessary to fill in this information.
This paper focuses on three aspects of population synthesis. After an overview of previous work (Section 2), the conventional approach (Beckman et al, 1996) is altered to support a larger number of attributes per agent (Section 3), adopting some ideas from an alternative reweighting approach (Williamson et al, 1998). Second, a new approach to relationship synthesis is proposed that allows person- and household-level agents to be synthesized with the correct geographic distribution of attributes at both levels simultaneously (Section 4). The new relationship method is also applicable to datasets without linkages between the person and household levels, such as the Canadian census. Third, the implications of “random rounding” in the Canadian census are briefly discussed (Section 5). Finally, the effects of varying amounts of input data on the synthesis procedure are evaluated (Section 6) and concluding remarks (Sections 7 and 8).
While the methods were developed to support the ILUTE integrated land use/transportation model (Salvini and Miller, 2005), this paper is relevant to a broad group of socioeconomic models that use microsimulation methods.
A three-way contingency table
![]() (or sometimes
(or sometimes
![]() )
cross-classifies variables
)
cross-classifies variables ![]() ,
, ![]() and
and ![]() into
into ![]() ,
, ![]() and
and ![]() categories
respectively.
Each cell
categories
respectively.
Each cell ![]() is a count of observations classified
into category
is a count of observations classified
into category ![]() of the first variable, category
of the first variable, category ![]() of the second variable and
category
of the second variable and
category ![]() of the third variable. The conventional notation
of the third variable. The conventional notation
![]() is used to indicate a one-way margin of
is used to indicate a one-way margin of
![]() .
Each cell
.
Each cell
![]() of this margin contains the number of
observations where variable
of this margin contains the number of
observations where variable ![]() was observed in category
was observed in category ![]() . The notation
. The notation
![]() is shorthand for
is shorthand for ![]() , the total number of observations in table
, the total number of observations in table
![]() . Variable
. Variable ![]() will consistently represent geographic
zones here.
will consistently represent geographic
zones here.
The IPF algorithm (Deming and Stephan, 1940) is a method for adjusting a source
contingency table (denoted with lower-case ![]() ) to match known marginal
totals for some target population (denoted with upper-case
) to match known marginal
totals for some target population (denoted with upper-case ![]() ).
First, a “source” population is sampled and cross-classified to form a multiway table
).
First, a “source” population is sampled and cross-classified to form a multiway table
![]() . A similarly
structured
multiway table
. A similarly
structured
multiway table
![]() is desired for some target population, but
less information is available about the target: typically, some marginal totals
is desired for some target population, but
less information is available about the target: typically, some marginal totals
![]() and
and
![]() are known.
The
complete multiway table
are known.
The
complete multiway table
![]() of the target population is
never known, but the IPF procedure is used to find an estimate
of the target population is
never known, but the IPF procedure is used to find an estimate
![]() . This is achieved through repeated modifications of the
table
. This is achieved through repeated modifications of the
table
![]() . The result is unique and
exactly satisfies the margins, except
in cases where entire rows/columns are zero in the source sample and non-zero
in the margin. The method extends
easily to higher dimensional tables cross-classifying more than two
variables, and also to higher-dimension margins (Deming and Stephan, 1940).
. The result is unique and
exactly satisfies the margins, except
in cases where entire rows/columns are zero in the source sample and non-zero
in the margin. The method extends
easily to higher dimensional tables cross-classifying more than two
variables, and also to higher-dimension margins (Deming and Stephan, 1940).
IPF minimizes discrimination information or relative entropy (Little and Wu, 1991). That is, the fitted table
![]() minimizes
minimizes
| (2) |
The IPF procedure is capable of operating in the presence of zeroes in either the source table or the margins. A zero cell in the source table can be either a “sampling zero” where the sample—by chance—did not contain any observations for a particular cell. Alternatively, the zero could be a “structural zero” where the cell will be zero regardless of the sample chosen, typically when a particular combination of categories is impossible. For example, the combination of “women aged 0-10” and “women with one child” would be a structural zero. Lacking any means of distinguishing sampling zeroes from structural zeroes, the IPF procedure will preserve zeroes from the source table in the fitted table.
The standard procedures for using IPF in population synthesis with PUMS data
were derived as part of the TRANSIMS project (Beckman et al, 1996). Essentially,
the PUMS data is used as the multiway source sample
![]() , Summary
Files are used to form the low-dimensional margins of
, Summary
Files are used to form the low-dimensional margins of
![]() and the IPF
procedure is used to adjust the source
sample to fit the margins, resulting in a fitted table
and the IPF
procedure is used to adjust the source
sample to fit the margins, resulting in a fitted table
![]() .
The original paper described two approaches for dealing with geography. In the
zone-by-zone approach, one zone is fitted at a time using the margins of
.
The original paper described two approaches for dealing with geography. In the
zone-by-zone approach, one zone is fitted at a time using the margins of
![]() for that zone alone. This assumes that every zone shares the
correlation structure of the PUMA defined in
for that zone alone. This assumes that every zone shares the
correlation structure of the PUMA defined in
![]() . The multizone
approach takes the opposite tack: all zones are fitted simultaneously by
adding a new dimension to the marginal table
. The multizone
approach takes the opposite tack: all zones are fitted simultaneously by
adding a new dimension to the marginal table
![]() for the zone
code. The details are a little convoluted, but Figure 1
provides a succinct explanation.
for the zone
code. The details are a little convoluted, but Figure 1
provides a succinct explanation.
The IPF process produces a multiway contingency table for the zones, where each
cell contains a real-valued count
![]() of the number of
agents with a particular set of attributes
of the number of
agents with a particular set of attributes ![]() and
and ![]() in zone
in zone
![]() . However, to
define a discrete set of agents integer counts are required. Deterministic
rounding of the counts is not a satisfactory “integerization” procedure for
three reasons: the rounded table may not be the best solution in terms of
discrimination information; the rounded table may not offer as good a fit to
margins as other integerization procedures; and rounding may bias the estimates,
particularly for cells representing “rare” characteristics with a count
under 0.5.
The original paper handled this problem by treating the fitted table as a
joint probability mass function (PMF), and then used
. However, to
define a discrete set of agents integer counts are required. Deterministic
rounding of the counts is not a satisfactory “integerization” procedure for
three reasons: the rounded table may not be the best solution in terms of
discrimination information; the rounded table may not offer as good a fit to
margins as other integerization procedures; and rounding may bias the estimates,
particularly for cells representing “rare” characteristics with a count
under 0.5.
The original paper handled this problem by treating the fitted table as a
joint probability mass function (PMF), and then used ![]() Monte Carlo
draws from this PMF to select
Monte Carlo
draws from this PMF to select ![]() individual cells (Beckman et al, 1996). These
draws can be
tabulated to give an integerized approximation
individual cells (Beckman et al, 1996). These
draws can be
tabulated to give an integerized approximation
![]() of
of
![]() . This is an effective way
to avoid biasing problems, but at the expense of introducing a nondeterministic step into the synthesis.
. This is an effective way
to avoid biasing problems, but at the expense of introducing a nondeterministic step into the synthesis.
![\includegraphics[width=4.8in]{figure_beckman}](figure_beckman.png)
|
There are several documented applications of the IPF method for population synthesis (Bowman, 2004).
The primary alternative to the Iterative Proportional Fitting algorithm is the reweighting approach (Williamson et al, 1998), also sometimes known as combinatorial optimization. Williamson et al proposed a zone-by-zone method with a different parameterization of the problem: instead of using a contingency table of real-valued counts, they chose a list representation with one row per PUMS entry, each with an integer weight. Within a single zone, they used weights of either zero or one on each PUMS row, allowing no replication of PUMS observations within a single zone.
To estimate the weights, they used various optimization procedures to find
the set of ![]() weights yielding the best fit to the Summary Tables for
a single zone. They considered several different measures of fit, and
compared different optimization procedures including hill-climbing,
simulated annealing and genetic algorithms.
By solving directly for integer weights, a better fit to the Summary Tables
might be obtained than with IPF methods where Monte Carlo
integerization step harms the fit.
weights yielding the best fit to the Summary Tables for
a single zone. They considered several different measures of fit, and
compared different optimization procedures including hill-climbing,
simulated annealing and genetic algorithms.
By solving directly for integer weights, a better fit to the Summary Tables
might be obtained than with IPF methods where Monte Carlo
integerization step harms the fit.
The reweighting approach has three primary weaknesses. First, the attribute
association observed in the PUMS (
![]() ) is not preserved by the
algorithm. The IPF method has an explicit formula defining the relationship
between the fitted table
) is not preserved by the
algorithm. The IPF method has an explicit formula defining the relationship
between the fitted table
![]() and the PUMS table
and the PUMS table
![]() in equation (3). Beckman et al.'s
multizone approach also treats the PUMS association pattern for the entire
PUMA as a constraint, and ensures that the full population matches that
association pattern. The reweighting method does operate on the PUMS, and
an initial random choice of weights will roughly match the association pattern
of the PUMS. However, the reweighting procedure does not make any effort to
preserve that association pattern.
in equation (3). Beckman et al.'s
multizone approach also treats the PUMS association pattern for the entire
PUMA as a constraint, and ensures that the full population matches that
association pattern. The reweighting method does operate on the PUMS, and
an initial random choice of weights will roughly match the association pattern
of the PUMS. However, the reweighting procedure does not make any effort to
preserve that association pattern.
Secondly, the reweighting method is very computationally expensive. When
solving for a single zone ![]() , there are
, there are ![]()
![]() weights, one for each
PUMS entry. However, this gives rise to
weights, one for each
PUMS entry. However, this gives rise to
![]() possible
combinations; Williamson et al (1998) called it “incredibly large.”
Of course, the optimization procedures are intelligent
enough to explore this space selectively and avoid an exhaustive search;
nevertheless, Huang and Williamson (2001) reported a runtime of 33 hours using an 800MHz
processor.
possible
combinations; Williamson et al (1998) called it “incredibly large.”
Of course, the optimization procedures are intelligent
enough to explore this space selectively and avoid an exhaustive search;
nevertheless, Huang and Williamson (2001) reported a runtime of 33 hours using an 800MHz
processor.
Finally, the reweighting method uses
![]() weights to represent a
weights to represent a
![]() -zone area. This parameter space is quite large; larger, in fact, than
the population itself. It is not surprising that good fits can be achieved
with a large number of parameters, but the method is not particularly
parsimonious and may overfit the Summary Tables. It is likely that
a simpler model with fewer parameters could achieve as good a fit, and
would generalize better from the small (2-5%) PUMS sample to the full population.
-zone area. This parameter space is quite large; larger, in fact, than
the population itself. It is not surprising that good fits can be achieved
with a large number of parameters, but the method is not particularly
parsimonious and may overfit the Summary Tables. It is likely that
a simpler model with fewer parameters could achieve as good a fit, and
would generalize better from the small (2-5%) PUMS sample to the full population.
For a microsimulation model spanning many aspects of society and the economy it is useful to be able to associate a range of attributes with each agent. Different attributes are useful for different aspects of the agent's behavior. For a person agent, labor force activity, occupation, industry and income attributes are useful for understanding his/her participation in the labor force. Meanwhile, age, marital status, gender and education attributes might be useful for predicting demographics.
However, as more attributes are associated with an agent, the number of
cells in the corresponding multiway contingency table grows exponentially.
A multiway contingency
table representing the association pattern between attributes has
![]() cells. If a new attribute with
cells. If a new attribute with ![]() categories is added, then
categories is added, then ![]() times more cells are needed. Asymptotically,
the storage space is exponential in the number of attributes. As a result,
fitting more than eight attributes with a multizone IPF procedure typically
requires more memory than available on a desktop computer. However, the
table itself is cross-classifying a fixed number of observations (i.e.,
a PUMS), and is extremely sparse when a large number of attributes are
included.
Is there a way to exploit this sparsity and synthesize a large number of
attributes?
times more cells are needed. Asymptotically,
the storage space is exponential in the number of attributes. As a result,
fitting more than eight attributes with a multizone IPF procedure typically
requires more memory than available on a desktop computer. However, the
table itself is cross-classifying a fixed number of observations (i.e.,
a PUMS), and is extremely sparse when a large number of attributes are
included.
Is there a way to exploit this sparsity and synthesize a large number of
attributes?
Sparsity is a familiar problem in numerical methods. Many branches of science store large sparse 2D matrices using special data structures that hold only the non-zero sections of the matrix, instead of using a complete array that includes cells for every zero. The IPF method itself has little impact on the sparsity pattern of a table, and does not require a complete representation of the table. After the first iteration of fits to the constraints, the final sparsity pattern is essentially known; some cells may eventually converge to near-zero values, but few other changes occur.
The benefits of using a sparse data structure are substantial:
efficient use of computer memory, flexibility of aggregation and easier linking of data
sources (Williamson et al 1998). In terms of efficiency,
the method described here allows the IPF algorithm to be implemented
using storage proportional to the number of non-zero cells in the initial
table. For agent synthesis with the zone-by-zone method, this is
proportional to ![]() (the number of observations in the PUMS) multiplied by
(the number of observations in the PUMS) multiplied by
![]() (the number of attributes to fit). The multizone method combines
several IPF stages, and requires considerably more memory: a similar
(the number of attributes to fit). The multizone method combines
several IPF stages, and requires considerably more memory: a similar
![]() in the first stage, but
in the first stage, but
![]() in the second
stage (expressed in order of magnitude terms using the “Big O” Landau
notation commonly used in computer science).
in the second
stage (expressed in order of magnitude terms using the “Big O” Landau
notation commonly used in computer science).
It is helpful to consider a real example: synthesis of family agents using the 1986 Family PUMS for the Toronto CMA, which contains 9,061 families. (This paper uses 1986 data only because it is the base year for the ILUTE land use/transportation model; this base year allows model validation over the 1986-2006 simulation period.) For synthesis of 10 attributes using a zone-by-zone method, the complete representation requires 52.5 MB of storage while a sparse scheme needs only 0.1 MB. When a multizone method is used for the 731 zones, complete storage would require a prohibitive 38,369 MB while sparse storage needs only 27 MB. For small numbers of attributes, however, the complete representation is more efficient.
There are many types of data structures that could be used to represent a
sparse high dimensional contingency table. The data structure proposed here
is not the most efficient, but is conceptually simple. It borrows directly
from the reweighting/combinatorial optimization method (Williamson et al, 1998):
the data is represented as a list of the PUMS microdata entries, with a
weight attached to each. The weight is an expansion factor, representing the
number of times to replicate that record to form a complete population.
While the representation used by the combinatorial optimization method includes
only integer weights and operates on a zone-by-zone basis, the approach used
here behaves exactly like IPF and hence allows fractional weights. With a small
extension, it can also support multiple zones: instead of attaching one
weight to each PUMS entry, ![]() weights are used. An
illustration of
the data structure is shown in Figure 2.
weights are used. An
illustration of
the data structure is shown in Figure 2.
Flexible aggregation is a real advantage of a list-based representation (Williamson et al 1998). Complete array storage is proportional to the number of categories used for each attributes, while the sparse storage scheme is not affected by the categorization of the attributes. Many applications of IPF that used complete arrays were forced to abandon detailed categorization schemes to conserve space and allow more attributes to be synthesized (see for example Arentze and Timmermans (2005); Auld et. al (2009)). This in turn makes it difficult to apply several margins, since different margins may categorize a single attribute differently. When a large number of categories are possible, however, the attribute can be represented with a fine categorization and collapsed on-the-fly to different coarse categorizations as required during the fitting procedure.
To implement the IPF algorithm with a sparse list structure, the following operations are necessary:
Since the target population margins remain stored as complete arrays, these
operations are relatively straightforward. The collapse operation can be
done in a single pass over the list, using the category numbers in each
list row as co-ordinates into the complete array that stores the collapsed
table. The update operation can likewise be done in a single pass over
the list. Both operations are fast with complexity equal to the
storage cost,
![]() .
.
Setting the initial weights requires a little more work and is slightly
counterintuitive. With a complete array representation, the initial table
is set to the PUMS cross-tabulation for a zone-by-zone synthesis and set to
a uniform distribution (1.0 in all cells) for multizone synthesis. In the
sparse representation used here, this changes slightly since there is one
weight per PUMS entry instead of groups of PUMS entries in each cell.
Consequently, the initial row weights need to be set to 1.0 for the
zone-by-zone method. For the multizone method, the sum of the weights
in the ![]() rows that contribute to a single cell in the equivalent
complete table needs to add to one, and the individual weights are
therefore
rows that contribute to a single cell in the equivalent
complete table needs to add to one, and the individual weights are
therefore ![]() . To allow easy calculation of
. To allow easy calculation of ![]() , the list needs to be
sorted by the table dimension co-ordinates, grouping the rows that
contribute to a single cell. Thus the initial weights can be set in
, the list needs to be
sorted by the table dimension co-ordinates, grouping the rows that
contribute to a single cell. Thus the initial weights can be set in
![]() time.
time.
Additionally, the multizone IPF procedure requires a fit to the distribution
of all non-geographic variables simultaneously.
(See the
![]() margin on the right half of
Figure 1.) This margin is
high-dimensional—it
includes all variables except for the geographic variable—but is also
stored as a sparse list with a single weight per row. This
weight can be treated as a constraint on the total for the weights in each
row, and suitable collapse/update procedures are then easily defined. The
computation cost is still
margin on the right half of
Figure 1.) This margin is
high-dimensional—it
includes all variables except for the geographic variable—but is also
stored as a sparse list with a single weight per row. This
weight can be treated as a constraint on the total for the weights in each
row, and suitable collapse/update procedures are then easily defined. The
computation cost is still
![]() for this type of constraint.
for this type of constraint.
Finally, integerization for this sparse structure is little changed. The list of weights (or 2D array of weights for multizone) is normalized and treated as a PMF and individual entries are synthesized using Monte Carlo draws.
This sparse data structure removes a substantial limitation from the
IPF algorithm, but also raises new questions. Is there a limit to the number of
attributes that can be synthesized? If there is a limit, how is it related
to the size ![]() of the PUMS sample?
of the PUMS sample?
The answers to these questions remain elusive. The issue likely hinges on the
statistical validity of high-dimensional contingency tables. These tables
are inherently sparse, with
a large fraction of the non-empty cells containing only one observation and
the number of cells is often much larger than the number of observations. In
other words, the sample does not provide a statistically meaningful
estimate of the probability distribution for such a high dimensional table.
However, the high-dimensional table can be collapsed to produce 2D or 3D
tables, each of which is adequately sampled and gives a statistically valid
distribution of counts. For example, in an 8-way cross-classification of a
1986 Toronto census PUMS containing 9,061 families, 99.7% of the
984,150 cells were zero. However, one of the table's three-way margins had
54 cells and a median of 30 observations per cell. There are
![]() possible choices of variables to form a 3-way margin of the 8-way
table, and the observations per cell in each margin is comparable.
Consequently, while a sparse 8-way table does not provide statistically
meaningful information about 8-variable interaction, it could be viewed as
a means of linking the many 2- or 3-way tables formed by its margins.
possible choices of variables to form a 3-way margin of the 8-way
table, and the observations per cell in each margin is comparable.
Consequently, while a sparse 8-way table does not provide statistically
meaningful information about 8-variable interaction, it could be viewed as
a means of linking the many 2- or 3-way tables formed by its margins.
In this section, the discussion shifts from a single agent type (e.g., family agents) to the synthesis of multiple agent types simultaneously: for example, person agents and household agents.
In the U.S. context, the relationship between these types of agents can be observed directly in the PUMS data. Synthesis of both types of agents typically uses a top-down approach, where households are created with IPF (fitting only against household-level attributes) and subsequently the links built into the U.S. PUMS are used to synthesize the individual persons within the households (Barrett et al, 2003; Beckman et al, 1996). The synthesized persons are naturally grouped into plausible households, because the procedure draws from observed groupings of persons in the PUMS.
By contrast, this approach is impossible in the Canadian census, where the PUMS for households contains only limited information on the persons within the household, and no way of linking to the detailed census data on individual persons. While Canadian data limitations were the original motivation for developing a new method, other benefits became apparent after the method was developed. For non-Canadian applications, the method offers two key advantages over the conventional approach to synthesizing households:
Several previous papers have attempted to deal with the issue of fitting against both household and person attributes. Guo and Bhat (2007) built on the conventional approach, retaining the U.S. census' linkage between households and persons, but modifying the Monte Carlo synthesis stage to attempt a fit at both the household level and the person level simultaneously. Only a few person-level attributes were incorporated: gender and age. The constraints were somewhat loose and ad hoc, since the procedure attempted to satisfy competing goals when trying to achieve a good fit at both the household and person levels.
Ye et al (2009) tackled the same problem of person-level attributes. They applied IPF twice independently, first on the household level and second on the person level, obtaining two separate sets of weights. A heuristic procedure was then used to solve for household-level weights that could simultaneously satisfy both IPF-derived sets of weights. The method showed good results in a case study with three attributes at both the household and person levels, but the authors acknowledged that both the total number of attributes and the number of categories per attribute play an important role in the performance of the algorithm. It is likely that the method would have difficulty with the large number of attributes and categories contemplated in this paper.
Arentze and Timmermans (2005) only synthesized for the top-level agent, the household. Their synthesis included the age and labor force activity of both husband and wife, and the number of children in the household. They did not connect this to a separate synthesis of persons with detailed individual attributes, but by synthesizing at an aggregate level they guaranteed that the population was consistent and satisfied key constraints between family members, in the same manner as Beckman et al (1996).
Guan (2002) used a bottom-up approach to build families using the Canadian census. The person agents were synthesized first, and then assembled to form families. Children were grouped together (and constrained to have similar ages), then attached to parents. Constraints between parent/child ages and husband/wife ages were included, although there are some drawbacks to the method used for enforcement. Guan likewise used a bottom-up approach to combine families and non-family persons into households.
Any method for synthesizing relationships between persons must produce credible groupings of persons (into families and/or households). Suppose that a population of person agents has been synthesized, with a limited amount of information about their relationships in families (such as an attribute FSTRUC, which classifies a person as married, a lone parent, a child living with parent(s), or a non-family person). In the absence of any information about how families form, the persons could be formed into families in a naïve manner: randomly select male married persons and attach them to female married persons, and randomly attach children to couples or lone parents. Immediately, problems would emerge: some persons would be associated in implausible manners, such as marriages with age differences over 50 years, marriages between persons living at opposite ends of the city, or parents who are younger than their children.
A well-designed relationship synthesis procedure should carefully avoid such problems. A good choice of relationships satisfies certain constraints between agents' attributes, such as the mother being older than her child, or the married couple living in the same zone. It also follows known probability distributions, so that marriages with age differences over 50 years have a low but non-zero incidence.
Most constraints and probability distributions are observed in microdata samples of aggregate agents such as families or households. A complete Family PUMS in the Canadian census includes the ages of mothers and children, and none of the records includes a mother who is younger than her children. Similarly, only a small fraction of the records include marriages between couples with ages differing by more than 50 years. The question, however, is one of method: how can relationships between agents be formed to ensure that the desired constraints are satisfied?
As Guo and Bhat (2007), Ye et al (2009) and Guan (2002) found, working at the
household/family and person levels simultaneously can introduce conflicts between the
competing goals of achieving good fit at both levels.
The family population may contain 50 husband-wife families in zone ![]() where
the husband has age
where
the husband has age ![]() , while the person population contains only 46
married males of age
, while the person population contains only 46
married males of age ![]() in zone
in zone ![]() . In the face of such
inconsistencies, either families or persons must be changed: a family
could be attached to a male of age
. In the face of such
inconsistencies, either families or persons must be changed: a family
could be attached to a male of age ![]() , or a person could be modified to
fit the family. In both cases, either the family or person population is deemed
“incorrect” and modified. The editing procedures are difficult to perform,
and inherently ad hoc. Furthermore, as the number of overlapping
attributes between the two populations grows, inconsistencies become
quite prevalent.
, or a person could be modified to
fit the family. In both cases, either the family or person population is deemed
“incorrect” and modified. The editing procedures are difficult to perform,
and inherently ad hoc. Furthermore, as the number of overlapping
attributes between the two populations grows, inconsistencies become
quite prevalent.
What are the sources of these inconsistencies? They come from two places:
first, the fitting procedure used to estimate the population distribution
![]() for persons and
for persons and
![]() for families may
not give the same totals for a given set of common attributes. Second, even if
for families may
not give the same totals for a given set of common attributes. Second, even if
![]() and
and
![]() could be made to agree on all
shared attributes, the populations produced by independent Monte Carlo
synthesis on the two tables (used by Guan) may not agree,
since the Monte Carlo procedure is non-deterministic. In the following
sections, a method is proposed to resolve these two issues.
could be made to agree on all
shared attributes, the populations produced by independent Monte Carlo
synthesis on the two tables (used by Guan) may not agree,
since the Monte Carlo procedure is non-deterministic. In the following
sections, a method is proposed to resolve these two issues.
For the purposes of discussion, consider a simple synthesis example:
synthesizing husband-wife families. Suppose that the universe of persons
includes all persons, with attributes for gender
![]() , family
status
, family
status
![]() , age
, age
![]() , education
, education
![]() and zone
and zone
![]() . The universe of families includes only
husband-wife couples, with attributes for the age of husband
. The universe of families includes only
husband-wife couples, with attributes for the age of husband
![]() and
wife
and
wife
![]() , and zone
, and zone
![]() . IPF has already been used
to estimate the contingency table cross-classifying persons
(
. IPF has already been used
to estimate the contingency table cross-classifying persons
(
![]() ) and likewise for the table of families
(
) and likewise for the table of families
(
![]() ). The shared attributes between the two
populations are age and zone, and implicitly gender. The two universes do
not overlap directly, since only a fraction of the persons belong
to husband-wife families; the others may be lone parents, children, or
non-family persons, and are categorized as such using the
). The shared attributes between the two
populations are age and zone, and implicitly gender. The two universes do
not overlap directly, since only a fraction of the persons belong
to husband-wife families; the others may be lone parents, children, or
non-family persons, and are categorized as such using the
![]() attribute.
attribute.
In order for consistency between
![]() and
and
![]() , the following must be met for
, the following must be met for
![]() and any choice of
and any choice of ![]() :
:
That is, the number of married males of age ![]() in zone
in zone ![]() must be the
same as the number of husband-wife families with husband of age
must be the
same as the number of husband-wife families with husband of age ![]() in zone
in zone
![]() . While this might appear simple, it is often not possible with the
available data. A margin
. While this might appear simple, it is often not possible with the
available data. A margin
![]() giving the
giving the
![]() distribution is probably available to apply to
the person population. However, a similar margin for just married males
is not likely to exist for the family population; instead, the age
breakdown for married males in the family usually comes from the PUMS
alone. As a result, equation (4) is not satisfied.
distribution is probably available to apply to
the person population. However, a similar margin for just married males
is not likely to exist for the family population; instead, the age
breakdown for married males in the family usually comes from the PUMS
alone. As a result, equation (4) is not satisfied.
One suggestion immediately leaps to mind: if the person population is
fitted with IPF first and
![]() is known,
the slice of
is known,
the slice of
![]() where
where
![]() and
and
![]() could be applied as a margin to the family
fitting procedure, and likewise for
could be applied as a margin to the family
fitting procedure, and likewise for
![]() . This is entirely
feasible, and does indeed guarantee matching totals between the
populations. The approach can be used for the full set of attributes shared
between the individual and family populations. There is one downside,
however: it can only be performed in one direction. The family table can be
fitted to the person table or vice versa, but they cannot be fitted
simultaneously.
. This is entirely
feasible, and does indeed guarantee matching totals between the
populations. The approach can be used for the full set of attributes shared
between the individual and family populations. There is one downside,
however: it can only be performed in one direction. The family table can be
fitted to the person table or vice versa, but they cannot be fitted
simultaneously.
Finally, there remains one wrinkle: it is possible that the family population will still not be able to fit the total margin from the individual population, due to a different sparsity pattern. For example, if the family PUMS includes no families where the male is 15-19 years old but the individual PUMS does include a married male of that age, then the fit cannot be achieved. This is rarely an issue when a small number of attributes are shared, but when a large number of attributes are shared between the two populations it is readily observed. The simplest solution is to minimize the number of shared attributes, or to use a coarse categorization for the purposes of linking the two sets of attributes.
Alternatively, the two PUMS could be cross-classified using the shared
attributes and forced to agree. For example, for
![]() and
and
![]() , then the pattern of zeros in
, then the pattern of zeros in
![]() and
and
![]() could be forced to agree by
setting cells to zero in one or both tables. (In the earlier example, this
would remove the married male of age 15-19 from the Person PUMS.) The person
population is then fitted using this modified PUMS, and the family
population is then fitted to the margin of the person population.
could be forced to agree by
setting cells to zero in one or both tables. (In the earlier example, this
would remove the married male of age 15-19 from the Person PUMS.) The person
population is then fitted using this modified PUMS, and the family
population is then fitted to the margin of the person population.
The second problem with IPF-based synthesis stems from the independent
Monte Carlo draws used to synthesize persons and families. For example,
suppose that mutually fitted tables
![]() and
and
![]() are used with Monte Carlo to produce a complete
population of persons and families
are used with Monte Carlo to produce a complete
population of persons and families
![]() and
and
![]() . If it can be guaranteed for
. If it can be guaranteed for
![]() and
and
![]() that
that
A simplistic solution would be a stratified sampling scheme: for each
combination of ![]() and
and ![]() , select a number of individuals to synthesize
and make exactly that many draws from the subtables
, select a number of individuals to synthesize
and make exactly that many draws from the subtables
![]() and
and
![]() . This approach
breaks down when the number of strata grows large, as it inevitably does
when more than one attribute is shared between persons and families.
. This approach
breaks down when the number of strata grows large, as it inevitably does
when more than one attribute is shared between persons and families.
The problem becomes clearer once the reason for mismatches is recognized.
Suppose a Monte Carlo draw selects a family with husband age ![]() in
zone
in
zone ![]() . This random draw is not synchronized with the draws from the
person population, requiring a person of age
. This random draw is not synchronized with the draws from the
person population, requiring a person of age ![]() in zone
in zone ![]() to be drawn;
the two draws are independent. Instead, synchronization could be achieved
by conditioning the person population draws on the family population
draws. Instead of selecting a random value from the joint
distribution
to be drawn;
the two draws are independent. Instead, synchronization could be achieved
by conditioning the person population draws on the family population
draws. Instead of selecting a random value from the joint
distribution
of the person population, a draw from the conditional distribution
could be used, and a similar draw for the wife. Converting the joint distribution generated by IPF to a conditional distribution is an extremely easy operation.
This reversal of the problem guarantees that equation (5) is satisfied, and allows consistent relationships to be built between agents. While it has been described here in a top-down manner (from family to person), it can be applied in either direction.
As demonstrated, it is possible to synthesize
persons and relate them together to form families, while still guaranteeing
that the resulting populations of persons and families approximately
satisfy the fitted tables
![]() and
and
![]() . By
carefully choosing a set of shared attributes between the person and
family agents and using conditional synthesis, a limited number of
constraints can be applied to the relationship formation process. In the
example discussed earlier, the ages of husband/wife were constrained; in a
more realistic example, the labor force activity of husband/wife, the
number of children and the ages of children might also be constrained.
Furthermore, multiple levels of agent aggregation could be defined: families
and persons could be further grouped into households and attached to
dwelling units.
. By
carefully choosing a set of shared attributes between the person and
family agents and using conditional synthesis, a limited number of
constraints can be applied to the relationship formation process. In the
example discussed earlier, the ages of husband/wife were constrained; in a
more realistic example, the labor force activity of husband/wife, the
number of children and the ages of children might also be constrained.
Furthermore, multiple levels of agent aggregation could be defined: families
and persons could be further grouped into households and attached to
dwelling units.
The synthesis order for the different levels of aggregation can be varied as required, using either a top-down or bottom-up approach. However, the method is still limited in the types of relationships it can synthesize: it can only represent nesting relationships. Each individual person can only belong to one family, which belongs to one household. Other types of relationships cannot be synthesized using this method, such as a person's membership in another group (e.g., a job with an employer).
While this method is clearly useful for Canadian data that lacks links between the household and person level, is it useful in other contexts? The answer depends on whether the benefits (simultaneous attribute fitting at the household and person level, and greater variation in household composition) outweigh the costs (implementation difficulty, and the synthetic nature of the household/person relationships).
Many census agencies apply random rounding procedures to published
tables, including the agencies in Canada, the United Kingdom and New
Zealand. Each agency has a base ![]() that it uses, and then modifies
a cell count
that it uses, and then modifies
a cell count ![]() by rounded up to the nearest multiple of
by rounded up to the nearest multiple of ![]() with a
probability
with a
probability ![]() , or down with a probability
, or down with a probability ![]() . In most applications, a
procedure called unbiased random rounding is used, where
. In most applications, a
procedure called unbiased random rounding is used, where
![]() . The alternative is called unrestricted random
rounding, where
. The alternative is called unrestricted random
rounding, where ![]() is constant and independent of the cell values; for
example, with
is constant and independent of the cell values; for
example, with ![]() it is equally likely that a cell will be rounded up
or down.
it is equally likely that a cell will be rounded up
or down.
For example, cells and marginal totals in Canadian census tables are
randomly rounded up or down to a multiple of ![]() using the unbiased
procedure. For a cell with a count of
using the unbiased
procedure. For a cell with a count of ![]() , there is a 20%
probability that it is published as
, there is a 20%
probability that it is published as
![]() and an 80%
probability that it is published as
and an 80%
probability that it is published as
![]() . Most importantly,
the expected value is equal to that of the unrounded count; it is therefore an
unbiased random rounding procedure.
. Most importantly,
the expected value is equal to that of the unrounded count; it is therefore an
unbiased random rounding procedure.
This can lead to conflicts between tables (Huang and Williamson, 2001): two different
cross-tabulations of the same variable or set of variables may be randomly
rounded to different values (for example, the ![]() margin of the
margin of the
![]() and
and
![]() tables). The
standard IPF procedure will not converge in this situation. The procedure
is also unable to take into account the fact that margins do not need to be
fitted exactly, since there is a reasonable chance that the correct count is
within
tables). The
standard IPF procedure will not converge in this situation. The procedure
is also unable to take into account the fact that margins do not need to be
fitted exactly, since there is a reasonable chance that the correct count is
within ![]() of the reported count.
of the reported count.
Two approaches were used in this work to deal with random rounding in the Canadian census data: a modification to the IPF termination criterion, and the use of hierarchical marginal tables.
For each cross-tabulation, statistical agencies publish a hierarchy
of margins, and these margins are rounded independently of the cells in the
table. For a three-way
table ![]() randomly rounded to give
randomly rounded to give
![]() ,
the data release will also include randomly rounded two-way margins
,
the data release will also include randomly rounded two-way margins
![]() ,
,
![]() and
and
![]() , one-way margins
, one-way margins
![]() ,
,
![]() and
and
![]() , and a zero-way
total
, and a zero-way
total
![]() . The sum of the cells does not necessarily match
the marginal total. For example, the sum
. The sum of the cells does not necessarily match
the marginal total. For example, the sum
![]() includes
includes
![]() randomly rounded counts. The expected value of this sum is the true
count
randomly rounded counts. The expected value of this sum is the true
count ![]() , but the variance is large and the sum could be off by as
much as
, but the variance is large and the sum could be off by as
much as ![]() in the worst case. By contrast, the reported marginal
total
in the worst case. By contrast, the reported marginal
total
![]() also has the correct expected value, but its
error is at most
also has the correct expected value, but its
error is at most ![]() .
.
For this reason, it seems sensible to include the hierarchical margins in the fitting procedure, in addition to the detailed cross-tabulation itself.
It is challenging to evaluate the results of a data synthesis procedure. If any form of complete “ground truth” were known, the synthetic population could be tested for goodness-of-fit against the true population's characteristics; instead only partial views of truth are available in smaller, four-way tables.
In theory, IPF-based procedures have many of the qualities necessary for a good synthesis: an exact fit to their margins, while minimizing the changes to the PUMS (using the discrimination information criterion). This does not mean that the full synthesis procedure is ideal: the fit will almost certainly be poorer after Monte Carlo (or conditional Monte Carlo). Furthermore, it still leaves a major question open: how much data is sufficient for a “good” synthesis? Are the PUMS and multidimensional margins both necessary, or could a good population be constructed with one of these two types of data? Does the multizone method offer a significant improvement over the zone-by-zone approach?
To investigate these questions, a series of experiments was conducted. The source data was from the 1986 census for the Toronto CMA, which is a single PUMA in the Canadian system. The synthetic population is a set of person agents with eight attributes each, described in Pritchard (2008). In the absence of ground truth, the synthetic population is evaluated in terms of its goodness-of-fit to a large collection of low-dimensional contingency tables. These validation tables are divided into the following groups:
After cross-classifying the synthetic population to form one table
![]() , it can be compared to a validation table
, it can be compared to a validation table
![]() using a goodness-of-fit statistic.
While there are sound theoretical reasons to prefer information-based statistics
like Minimum Discrimination Information (equivalent to the
using a goodness-of-fit statistic.
While there are sound theoretical reasons to prefer information-based statistics
like Minimum Discrimination Information (equivalent to the ![]() statistic in log-linear models), distance-based metrics are more common in
the literature.
The Standardized Root Mean Square Error (SRMSE) statistic was
chosen as a good distance-based metric for measuring matrix goodness-of-fit
(Knudsen and Fotheringham, 1986). Its formula is given by
statistic in log-linear models), distance-based metrics are more common in
the literature.
The Standardized Root Mean Square Error (SRMSE) statistic was
chosen as a good distance-based metric for measuring matrix goodness-of-fit
(Knudsen and Fotheringham, 1986). Its formula is given by
| SRMSE | 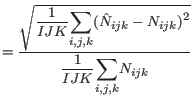 |
(6) |
This statistic is calculated for each of the validation tables in turn and the goodness-of-fit statistics in each group are then averaged together to give an overall goodness-of-fit for the group.
In the first series of experiments, the IPF procedure is tested with different inputs to see how the quality of fit is affected. Three questions are tested simultaneously using a set of ten fits, labeled I1 through I10. The input data included in each experiment are shown together with the output goodness-of-fit in Table 1. I6 represents a “typical” application of IPF for population synthesis: a zone-by-zone approach using 1D margins.
| Inputs | Method | Output | |||||||||||||||||||||||
| SRMSE × 1000 by table, | |||||||||||||||||||||||||
| Margins | grouped and averaged | ||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
| I1 | ✓ | 1 | none | 1 | 285 | 192 | 566 | 883 | |||||||||||||||||
| I2 | ✓ | PUMS | none | 0 | 285 | 15 | 522 | 38 | |||||||||||||||||
| I3 | ✓ | ✓ | 1 | none | 1 | 285 | 2 | 522 | 735 | ||||||||||||||||
| I4 | ✓ | ✓ | PUMS | none | 1 | 285 | 2 | 522 | 6 | ||||||||||||||||
| I5 | ✓ | 1 | one | 4 | 2 | 187 | 252 | 849 | |||||||||||||||||
| I6 | ✓ | PUMS | one | 1 | 3 | 19 | 130 | 73 | |||||||||||||||||
| I7 | ✓ | ✓ | 1 | one | 2 | 2 | 7 | 3 | 659 | ||||||||||||||||
| I8 | ✓ | ✓ | PUMS | one | 1 | 1 | 3 | 3 | 56 | ||||||||||||||||
| I9 | ✓ | ✓ | ✓ | 1 | multi | 0 | 3 | 15 | 131 | 38 | |||||||||||||||
| I10 | ✓ | ✓ | ✓ | ✓ | ✓ |
1 | multi | 0 | 1 | 0 | 3 | 0 | |||||||||||||
| M0 | ✓ | ✓ | ✓ | ✓ | ✓ |
1 | multi | 0 | 1 | 0 | 3 | 0 | |||||||||||||
| M1 | ✓ | ✓ | ✓ | ✓ | ✓ |
1 | multi | ✓ | 3 | 39 | 3 | 80 | 12 | ||||||||||||
| M2 | ✓ | ✓ | ✓ | ✓ | ✓ |
1 | multi | ✓ | 8 | 58 | 7 | 99 | 21 | ||||||||||||
|
|
|||||||||||||||||||||||||
The second series of experiments tests the effects of both the conventional Monte Carlo integerization procedure and the conditional Monte Carlo for relationships.
| Household |
| Zone × Dwelling type × Tenure |
| Zone × Dwelling type × Num. persons |
| Zone × Dwelling type × Dwelling age |
| Zone × Dwelling type × Num. rooms |
| Zone × Dwelling payments × Num. families × Tenure |
| Zone × Num. families × Num. persons |
| Family |
| Zone × Family structure × Num. children |
| Zone × Num. children aged 0-5 × 6-14 × 15-17 × 18-24 × 25+ |
| Zone × Num. children aged 0-5 × 6+ × Labor activity (female) |
| Person |
| Zone × Sex × Income |
| Zone × Sex × Age × Family status |
| Zone × Sex × Age × Labor activity |
| Zone × Sex × Age × Education |
| Zone × Sex × Education × Labor activity |
| Zone × Sex × Occupation |
The design and results of these experiments are also in Table 1 under labels M0-M2. Because the Monte Carlo procedure is non-deterministic, the reported SRMSE is an average over 30 trials. The first experiment M0 is the null case: IPF before Monte Carlo. Experiment M1 shows the conventional Monte Carlo procedure, where a set of persons are synthesized directly from the IPF-fitted table for persons. Experiment M2 is a top-down conditioned Monte Carlo procedure, where households/dwellings are synthesized by Monte Carlo, families are conditionally synthesized on dwellings, and persons are conditionally synthesized on families. The results are evaluated on the person population only, to focus on the effects of the two stages of conditioning prior to generating the persons. The dwellings had ten attributes each, families had fifteen attributes (one shared with both dwellings and persons, four shared only with dwellings and two shared only with persons). The full set of input margins used are shown in Table 2. An overview of the M2 population synthesis procedure is shown in Figure 3. The numbered steps shown in the figure are (with compute times as indicated):
![\includegraphics[width=4.8in]{figure_imp_overview}](figure_imp_overview.png)
|
As expected, the goodness-of-fit deteriorates after applying Monte Carlo, and deteriorates further using the conditional procedure. The deterioration from M0 to M1 is somewhat larger than the deterioration from M1 to M2. In essence, this shows that the conditional synthesis procedure employed here does not have a major impact on the goodness-of-fit. Even after two stages of conditioning (from dwellings to families to persons), a reasonable goodness-of-fit is maintained.
The IPF routines were implemented using special-purpose software on the R statistical computing platform (Ihaka and Gentleman, 1996) with a few routines in C. The total compute time for experiment M2 was two hours and seven minutes, running on an older 1.5 GHz computer with 2 GB of memory.
The data used for the experiments was the 1986 census of the Toronto Census Metropolitan Area (CMA). The census summary tables provide information about individual attributes in 731 census tracts (CTs) within the CMA, most of which are shown in Table 2. The associated PUMS datasets correspond to the entire CMA, and consist of:
Two additions to the existing procedure for population synthesis have been proposed in this paper. The sparse storage technique yields clear advantages in memory usage for large numbers of attributes, while retaining all of the theoretical advantages of an IPF-based procedure. The conditional Monte Carlo synthesis procedure allows a simultaneous fit to household, family and person level data and permits a valid synthesis of relationships between agents for non-U.S. census data. The evaluation demonstrates that this conditional procedure has only a minor impact on goodness-of-fit relative to the conventional Monte Carlo approach.