2 Notation

In this paper, I will use the symbol ${\bf I}$ to denote an identity matrix. The symbol ${\bf I}_s$ refers to a vector containing the $s$ th column of the identity matrix. To denote the skew-symmetric matrix form of a vector cross product, I will use the notation

$$S({\bf v}) = \begin{pmatrix} 0 & -{\bf v}_z & {\bf v}_y \\ {\bf v}_z & 0 & -{\bf v}_x \\ -{\bf v}_y & {\bf v}_x & 0 \end{pmatrix}$$

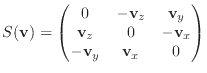
I will also define the vector $S_s({\bf v})$ as the transpose of the $s$ th row of $S({\bf v})$ . $S_s$ is a column vector, but represents a row in the original $S$ matrix. I will use a hat (e.g. ${\bf {\hat w}}_u$ ) to refer to a normalised vector of unit length, and omit the hat (e.g. ${\bf w}_u$ ) for an unnormalised vector. This is the opposite convention to that used in my original project report.

I will retain Baraff & Witkin's notation and use ${\bf x}$ to refer to the positions of points, not ${\bf p}$ as in Macri's paper. Furthermore, I will refer to the points of a triangle as ${\bf x}_0$ , ${\bf x}_1$ and ${\bf x}_2$ , and not use the $i$ , $j$ and $k$ subscripts used by the other two papers. For the points of an edge, I will likewise use subscripts of 0, 1, 2, and 3 rather than the $h$ , $i$ , $j$ and $k$ subscripts used by Macri.

When referring to points, I will use ${\bf x}_m$ and ${\bf x}_n$ to refer to two possibly distinct points. I will use the subscript $m_s$ to refer to the to the $s$ th component of ${\bf x}_m$ , and likewise the subscript $n_t$ for the $t$ th component of ${\bf x}_n$ . I will also sometimes use subsubscripts of $x$ , $y$ and $z$ to refer to the components.

I like to think of the derivatives in this paper in terms of their components. Both Baraff & Witkin and Macri differentiate with respect to a vector in their papers, giving quantities like

$$\frac{\partial C}{\partial {\bf x}_m} = \begin{pmatrix}\frac{\partial C}{\partial {\bf x}_{m_x}} \\ \fr... ...rtial {\bf x}_{m_y}} \\ \frac{\partial C}{\partial {\bf x}_{m_z}} \end{pmatrix}$$

or

$$\frac{\partial {\bf v}}{\partial {\bf x}_m} = \begin{pmatrix}\frac{\partial {\bf v}_x}{\partial {\bf x}_{m_x}... ...\bf x}_{m_z}} & \frac{\partial {\bf v}_z}{\partial {\bf x}_{m_z}} \end{pmatrix}$$

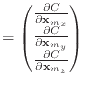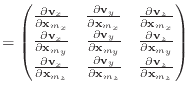This type of formula is common in some areas of graphics; for example, the Jacobian matrix has this form. However, what happens when we take the second derivative of ${\bf v}$ ? It will yield a third-order tensor, a $3\times3\times3$ linear algebraic quantity. However, this is unnecessarily complicated, especially for people (like me) who never covered tensors in their undergraduate education. In this paper, I will try to avoid differentiation with respect to a vector. Instead, I will do most of the work on a component-by-component basis, using only differentiation with respect to a scalar. Using this approach, I will only ever need to use vectors and scalars, not matrices or higher-order tensors. This makes operations such as cross-products and dot-products straightforward.

Some of Baraff & Witkin's formulas involve taking a second derivative with respect to two vectors. For these, just remember the layout of the resulting matrix. For example,

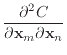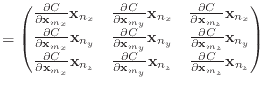$$\frac{\partial^2 C}{\partial {\bf x}_m \partial {\bf x}_n} = \begin{pmatrix}\frac{\partial C}{\partial {\bf x}_{m_x}} {{\bf ... ...n_z}} & \frac{\partial C}{\partial {\bf x}_{m_z}} {{\bf x}_{n_z}} \end{pmatrix}$$